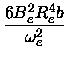


Next: 3. Results and Discussion
Up: Performance of the Effective-characteristic-polynomial
Previous: 1. Introduction
2. Methods
The ab initio MP4 and CCSD(T) calculations were done using the Gaussian 94
program package [23]. For all systems under study, we calculate
properties of the lowest singlet state.
For the MP energy terms, we used
|
(1) |
|
E2 = E(MP2) - E(SCF) |
|
|
(2) |
|
E3 = E(MP3) - E(MP2) |
|
|
(3) |
|
E4 = E(MP4SDTQ) - E(MP3). |
|
Then,
the F4 energy is given by
|
(4) |
F4 = E(SCF) + 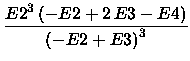
|
and the [2/2] energy is
|
(5) |
[2/2] = E(SCF) - 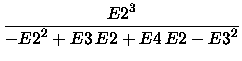 . .
|
The Padé approximation defined in (5) is obtained converting the formal power series
E0 + E1 z + E2 z2 + E3 z3 + E4 z4 + ... with E0 = E(SCF) and E1 = 0 to a [2/2] Padé approximant
followed by setting z = 1.
The  2 approximation is given by
The above mentioned criterion for the usability
of the MP series and the derived energies F4, [2/2], and
2 approximation is given by
The above mentioned criterion for the usability
of the MP series and the derived energies F4, [2/2], and  2 is
that the total variation of the latter three energies given by
2 is
that the total variation of the latter three energies given by
|
(7) |
 : = max( : = max(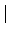 F4 - [2/2] F4 - [2/2]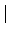 , ,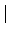 [2/2] - [2/2] - 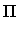 2 2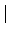 , ,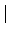 F4 - F4 - 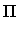 2 2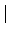 ) )
|
satisfies
|
(8) |
 < 5 mH . < 5 mH .
|
The results of
the calculations presented in [8] are summarized in
Figure 1. It is seen that the above criterion enforces that for the
accepted cases the errors are indeed of the order of 5 mH. If one would
not take
the criterion (8) into account, the errors are much larger as
shown in Figure 1.
Correlation energies are obtained either by regarding
the inner electrons as an effective potential (frozen core option) or dealing with all electrons
(full core option)
3.
In the single point calculations with different basis sets some basis sets were used
which are not included in Gaussian 94 via the
EMSL Gaussian Basis Set Order
Form
[24].
The potential surfaces of the diatomic molecules were calculated
with the Gaussian 94 program [23].
A 6-311G basis was chosen since the single-point calculations show
that this produces a rather satisfactory approximation of
the energies on the one hand, and is expected to be applicable to
much larger molecules, on the other hand. For the calculations of
spectroscopic constants three different approaches were examined.
Two fits of a narrow region around the minimum by polynomials of degree 3 or 5
were used to calculate
the five spectroscopic constants
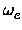 ,
,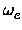 xe, Be,
xe, Be,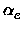 , De, the equilibrium distance Re, the force constant
ke and the minimum total electronic energy Ue.
The third approach using a four parameter Morse potential as fit function yielded
the two constants
, De, the equilibrium distance Re, the force constant
ke and the minimum total electronic energy Ue.
The third approach using a four parameter Morse potential as fit function yielded
the two constants
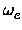 and
and
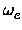 xe.
xe.
The calculated spectroscopic constants arise from a second order approximation of the rovibrational energy
as follows:
|
(9) |
Etot(v, J) = Evib(v) + Erot(v, J)
|
with
|
(10) |
Evib(v) = 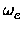 (v + (v + 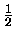 ) - ) - 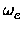 xe(v + xe(v + 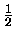 )2 )2
|
and
|
(11) |
Erot(v, J) = BvJ(J + 1) - DvJ2(J + 1)2
|
where
|
(12) |
Bv = Be - 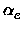 (v + (v + 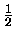 ) )
|
and
|
(13) |
Dv = De + 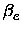 (v + (v + 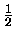 ). ).
|
For the notation of the various spectroscopic constants we followed the monograph of Hurley
[25, chapter 1.4].
The centrifugal distortion constant De should not be confused either with the
dissociation energy
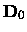 or the depth
or the depth
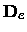 of the potential at the minimum.
of the potential at the minimum.
The Morse data were obtained by a least square fit of a Morse potential
|
(14) |
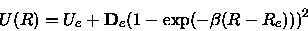 |
with fit parameters
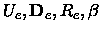 to a suitable part of the calculated potential surface that was
chosen according to the above criterion (8).
A Fortran 77 program which used the NAG [26] routine E04FDF
was used in the fitting procedure.
We follow the spectroscopic praxis
and choose cm-1 as unit for energies and frequencies in formulas and tables.
The vibrational frequency
to a suitable part of the calculated potential surface that was
chosen according to the above criterion (8).
A Fortran 77 program which used the NAG [26] routine E04FDF
was used in the fitting procedure.
We follow the spectroscopic praxis
and choose cm-1 as unit for energies and frequencies in formulas and tables.
The vibrational frequency 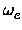 and the first anharmonicity constant were then calculated
from the parameters of the Morse potential using the formulas
and
and the first anharmonicity constant were then calculated
from the parameters of the Morse potential using the formulas
and
|
(16) |
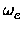 xe = xe = 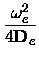
|
where 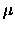 is the reduced mass of the diatomic molecule.
is the reduced mass of the diatomic molecule.
The least square fitting of the polynomials to the potential curves was done using Maple
[27],[28].
From the coefficients Re,ke,a,b of the fitted polynomial
|
(17) |
U(x) = Ue + 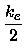 (x - Re)2 - a(x - Re)3 + b(x - Re)4 + c(x - Re)5 (x - Re)2 - a(x - Re)3 + b(x - Re)4 + c(x - Re)5
|
the spectroscopic constants were
calculated in the following way [25, chapter 1.4]
|
(19) |
Be = 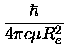
|
|
(22) |
De = 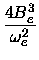
|
In the case of a polynom fit of third degree we set in Eq.(17) b = 0 and c = 0.



Next: 3. Results and Discussion
Up: Performance of the Effective-characteristic-polynomial
Previous: 1. Introduction
Herbert H. H. Homeier (herbert.homeier@na-net.ornl.gov)
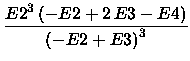

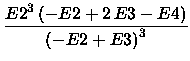
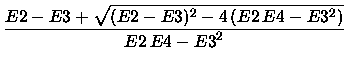
![]() ,
,![]() xe, Be,
xe, Be,![]() , De, the equilibrium distance Re, the force constant
ke and the minimum total electronic energy Ue.
The third approach using a four parameter Morse potential as fit function yielded
the two constants
, De, the equilibrium distance Re, the force constant
ke and the minimum total electronic energy Ue.
The third approach using a four parameter Morse potential as fit function yielded
the two constants
![]() and
and
![]() xe.
xe.
![]() or the depth
or the depth
![]() of the potential at the minimum.
of the potential at the minimum.
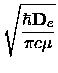
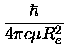
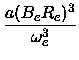 - 6
- 6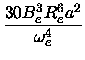 -
-